Олимпиадная задача по планиметрии: сумма углов между касательными в треугольнике
Задача
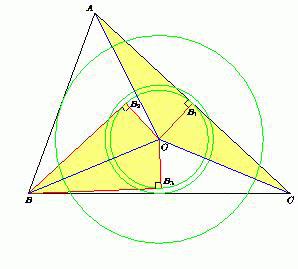
Пусть O – центр описанной окружности остроугольного треугольника ABC, SA, SB, SC – окружности с центром O, касающиеся сторон BC, CA и AB соответственно. Докажите, что сумма трёх углов: между касательными к SA, проведёнными из точки A, к SB – из точки B, и к SC – из точки C, равна 180°.
Решение
Пусть окружность с центром O касается стороны AC в точке B1, а касательных к этой окружности, проведённых из точки B, – в точках B2 и B3. Тогда прямоугольные треугольники BOB2, BOB3, AOB1 и CO1 равны по катету (радиус этой окружности) и гипотенузе (радиус описанной окружности треугольника ABC). Поэтому ∠B2BB3 = ∠OAC + ∠OCA.
Аналогично остальные два угла равны ∠OAB + ∠OBA и ∠OBC + ∠OCB. Следовательно, сумма трёх углов, о которых говорится в условии задачи, равна
(∠OAC + ∠OCA) + (∠OAB + ∠OBA) + (∠OBC + ∠OCB) = (∠OAC + ∠OAB) + (∠OCA + ∠OCB) + (∠OBC + ∠OBA) = ∠BAC + ∠ACB + ∠ABC = 180°.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь