Олимпиадная задача по планиметрии: параллелограмм ADKE в треугольнике ABC
Задача
В остроугольном треугольнике ABC через центр O описанной окружности и вершины B и C проведена окружность S. Пусть OK – диаметр окружности S, D и E – соответственно точки её пересечения с прямыми AB и AC. Докажите, что ADKE – параллелограмм.
Решение
Без ограничения общности рассмотрим случай, когда точка D лежит на стороне AB, а точка E – на продолжении стороны AC за точку C (см. рис.). Обозначим ∠A = α. Тогда ∠BOC = 2α, ∠OBC = ∠OCB = 90° – α.
Поскольку точка E лежит на окружности с диаметром OK, то
∠OEK = 90°, а так как вписанные в окружность S углы OEC и OBC опираются на одну дугу, то ∠OEC = ∠OBC = 90° – α. Поэтому ∠AEK = 90° + 90° – α = 180° – α. Значит, AD || KE. Аналогично, AE || DK.
Следовательно, ADKE – параллелограмм. 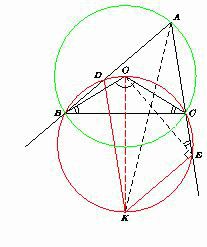
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь