Олимпиадная задача Блинкова по планиметрии: деление стороны квадрата биссектрисой
Задача
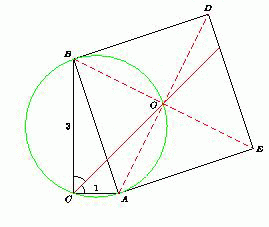
На гипотенузе AB прямоугольного треугольника ABC во внешнюю сторону построен квадрат ABDE. Известно, что AC = 1, BC = 3.
В каком отношении делит сторону DE биссектриса угла C?
Решение
Решение 1:Пусть O – центр данного квадрата. Точки C и O лежат на окружности с диаметром AB (рис. слева). Из равенства хорд AO и BO следует равенство вписанных углов ACO и BCO, поэтому луч CO – биссектриса угла C. Значит, прямая CO делит сторону AB квадрата на отрезки, отношение которых равно отношению сторон AC и BC треугольника ABC, то есть 1 : 3. Поскольку эта прямая проходит через центр квадрата, то она делит противоположную сторону DE в том же отношении.
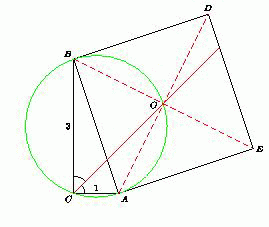
Решение 2:Приложим к квадрату еще три треугольника, равных ABC (рис. справа). Ясно, что образуется квадрат размера 4×4. Так как картинка, очевидно, симметрична относительно центра этого квадрата, а биссектриса угла C совпадает с диагональю CF, то она делит отрезок DE в том же отношении, что и гипотенузу AB, то есть в отношении AC : BC.
Ответ
1 : 3.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь