Задача по олимпиадной математике: восьмиугольник и квадраты, 8-9 класс, планиметрия

Задача

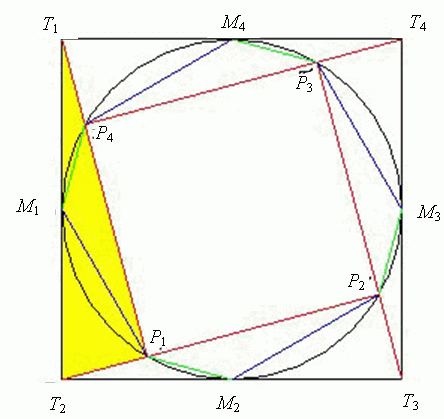
Известно, что вершины квадрата T принадлежат прямым, содержащим стороны квадрата P, а вписанная окружность квадрата T совпадает с описанной окружностью квадрата P. Найдите углы восьмиугольника, образованного вершинами квадрата P и точками касания окружности со сторонами квадрата T, и величины дуг, на которые вершины восьмиугольника делят окружность.

Решение

Введём обозначения так, как показано на рисунке.

УголP₁M₂P₂восьмиугольника опирается на дугу, равную 270°. Значит, он равен 135°. При повороте на угол 90° вокруг центра окружности вся фигура переходит в себя, поэтому меньшие дугиP₄M₁иP₁M₂равны. Следовательно, ∠M₁P₁M₂= 90° + ∠M₁P₁T₄+ ∠M₂P₁P₂= 90° + 45° = 135°. ПосколькуM₁P₁– медиана прямоугольного треугольникаT₁P₁T₂, то M₁P₁= ½T₁T₂, то есть хордаM₁P₁равна радиусу окружности. Значит, меньшая дугаM₁P₁равна 60°, а меньшая дугаP₁M₂равна l90° – 60° = 30°.

Ответ

Углы восьмиугольника равны 135°, дуги равны 30° и 60°.

Олимпиадная задача по планиметрии для 8-9 классов от Маркелова С. В.

Задача

Решение

Ответ

Подтверждение удаления