Олимпиадная задача по планиметрии для 8-9 классов о биссектрисе, точке P и окружности
Задача
Биссектриса угла A треугольника ABC пересекает описанную окружность в точке D. Пусть P – точка, симметричная центру вписанной окружности треугольника ABC относительно середины стороны BC, M – вторая точка пересечения прямой DP с описанной окружностью. Докажите, что расстояние от точки M до одной из вершин A, B, C равно сумме расстояний от M до двух других вершин.
Решение
Обозначим через I центр вписанной окружности треугольника ABC. Пусть R – радиус описанной окружности треугольника ABC, а DB = r. Как известно,
DC = DI = DB (см. задачу 153119).
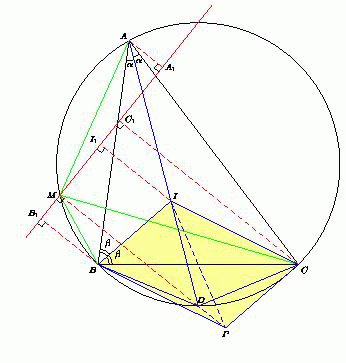
Через точку M проведём прямую k, перпендикулярную DM. Пусть I1, A1, B1 и C1 – проекции точек I, A, B и C на эту прямую. Тогда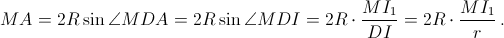 
Аналогично вычисляя MB и MC, получаем, что MA : MB : MC = MI1 : MB1 : MC1.
Поскольку точка P симметрична точке I относительно середины стороны BC, то BICP – параллелограмм. Отрезки MB1, MC1 и MI1 – проекции соответственно сторон BP, CP и диагонали IP этого параллелограмма на прямую k. Одна из этих проекций равна сумме двух других (на нашем рисунке MC1 = MI1 + C1I1 = MI1 + MB1 = B1I1), откуда и следует утверждение задачи.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь