Олимпиадная задача по планиметрии для 8–9 классов от Кулагина Д. Е.
Задача
На каждой стороне параллелограмма выбрано по точке (выбранные точки отличны от вершин параллелограмма). Точки, лежащие на соседних (имеющих общую вершину) сторонах, соединены отрезками. Докажите, что центры описанных окружностей четырёх получившихся треугольников – вершины параллелограмма.
Решение
Пусть точки M, N, P и Q лежат на сторонах соответственно AB, BC, CD и AD параллелограмма ABCD,
OA, OB, OC, OD – центры описанных окружностей треугольников AMQ, BMN, CNP, DPQ. Серединный перпендикуляр к отрезку XY будем обозначать через lXY. Пусть L – точка пересечения прямых lAQ и lMB, T – точка пересечения прямых lDQ и lCP. При параллельном переносе на вектор  прямая lAQ переходит в параллельную ей прямую, проходящую через точку T, то есть в прямую lDQ, а прямая lMB – в прямую lCP. Расстояние между параллельными прямыми lAM и lBM равно расстоянию между прямыми lCP и lDP (каждое из этих расстояний равно половине стороны AB). Значит, при рассматриваемом параллельном переносе прямая lAM переходит в прямую lPD. Аналогично при этом же переносе прямая lBN переходит в
прямую lCN. Из доказанного следует, что параллелограмм, образованный пересечением прямых lAM, lBM, lAQ и lBN переходит в параллелограмм,
образованный пересечением прямых lDP, lCP, lDQ и lCN. Поэтому диагональ OAOB первого из этих параллелограммов
переходит в соответствующую диагональ ODOC
второго. Следовательно, четырёхугольник OAOBOCOD – параллелограмм.
прямая lAQ переходит в параллельную ей прямую, проходящую через точку T, то есть в прямую lDQ, а прямая lMB – в прямую lCP. Расстояние между параллельными прямыми lAM и lBM равно расстоянию между прямыми lCP и lDP (каждое из этих расстояний равно половине стороны AB). Значит, при рассматриваемом параллельном переносе прямая lAM переходит в прямую lPD. Аналогично при этом же переносе прямая lBN переходит в
прямую lCN. Из доказанного следует, что параллелограмм, образованный пересечением прямых lAM, lBM, lAQ и lBN переходит в параллелограмм,
образованный пересечением прямых lDP, lCP, lDQ и lCN. Поэтому диагональ OAOB первого из этих параллелограммов
переходит в соответствующую диагональ ODOC
второго. Следовательно, четырёхугольник OAOBOCOD – параллелограмм.
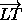
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь