Олимпиадная задача по планиметрии: точки пересечения и хорды окружности
Задача
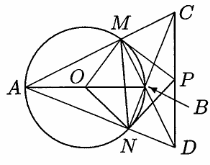
Дана фиксированная хорда MN окружности, не являющаяся диаметром. Для каждого диаметра AB этой окружности, не проходящего через точки M и N, рассмотрим точку C, в которой пересекаются прямые AM и BN, и проведём через неё прямую l, перпендикулярную AB. Докажите, что все прямые l проходят через одну точку.
Решение
Пусть O – центр нашей окружности Ω, D – точка пересечения AN и BM. Поскольку из точек M и N диаметр AB виден под прямым углом, то AN и BM – высоты треугольника ABC, а D – его ортоцентр. Следовательно, CD ⊥ AB. Значит, CD – одна из прямых l. Рассмотрим окружность девяти точек треугольника ABC. Как известно, середина P отрезка CD диаметрально противоположна середине O стороны AB, то есть прямая l проходит через точку P пересечения касательных, проведенных к окружности Ω в точках M и N.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь