Олимпиадная задача по планиметрии: треугольник ANK в правильном треугольнике ABC
Задача
На дуге AC описанной окружности правильного треугольника ABC взята точка M, отличная от C, P – середина этой дуги. Пусть N – середина хорды BM, K – основание перпендикуляра, опущенного из точки P на MC. Докажите, что треугольник ANK правильный.
Решение
При повороте на угол 60° вокруг точки A точка C переходит в точку B, точка P – в центр O описанной окружности, луч CM – в луч BM (так как
∠ABM = ∠ACM), прямая PK , перпендикулярная MC, – в прямую, проходящую через точку O перпендикулярно BM. Поскольку перпендикуляр, опущенный из центра окружности на хорду BM, проходит через её середину N, то точка K при рассматриваемом повороте переходит в точку N. Следовательно, треугольник ANK равносторонний. 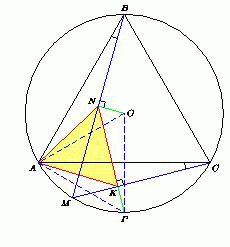
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь