Геометрическое место середин: олимпиадная задача по планиметрии для 8–9 классов

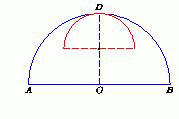
Пусть O – центр, а D – середина полуокружности Г. Построим квадраты ACKL и BCNP. Очевидно, AKNB – равнобочная трапеция, а C – точка пересечения ее диагоналей. Нас интересует середина M средней линии этой трапеции.  ∠ACM = 45°  или 135°, значит, прямая CM проходит через D. Треугольник COD – равнобедренный, поэтому его высота OM совпадает с медианой,то есть  DM = ½ DC.  Итак, точка M получена из точки C гомотетией с центром D и коэффициентом ½. Следовательно, искомое ГМТ есть полуокружность, полученная из Г (без точек A и B) этой гомотетией (см. рисунок в ответе).