Олимпиадная задача по математике: высота в треугольнике для 8

Олимпиадная задача по планиметрии для 8–9 класса: высота в остроугольном треугольнике

Длины сторон остроугольного треугольника – последовательные целые числа.

Докажите, что высота, опущенная на среднюю по величине сторону, делит её на отрезки, разность длин которых равна 4.

Пусть стороны треугольника равны n – 1, n и n + 1, отрезки, на которые высота делит основание, – x и y, высота – h. (см. рисунок).

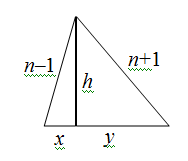
Тогда (y – x)n= (y – x)(y + x) =y² –x² = (y² +h²) – (x² +h²) = (n+ 1)² – (n– 1)² = 4n. Отсюда y – x= 4.

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Комментариев нет

Олимпиадная задача по планиметрии для 8–9 класса: высота в остроугольном треугольнике