Олимпиадная задача по планиметрии: доказательство о центре вписанной окружности в треугольнике (8-9 класс)
Задача
Внутри треугольника ABC взята такая точка M, что ∠BMC = 90° + ½ ∠BAC и прямая AM содержит центр O описанной окружности треугольника BMC. Докажите, что точка M – центр вписанной окружности треугольника ABC.
Решение
Продолжим отрезок AM за точку M до пересечения c этой окружностью в точке P. Если ∠BAC = 2α, то ∠BMC = 90° + α.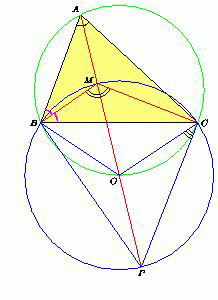 
ПосколькуBMCиBPC– противоположные углы вписанного четырёхугольникаBMCP, аBOC– центральный
угол, то
∠BOC= 2(180° – (90° + α)) =
180° – 2α. Значит, ∠BOC+ ∠BAC= 180°. Поэтому точкаOлежит на описанной окружности треугольникаABC. ПосколькуAOC– внешний угол равнобедренного треугольникаCOP, то ∠ABC= ∠AOC= 2∠OPC= 2∠MPC= 2∠MBC. Значит, точкаMлежит на биссектрисе углаABC.
АналогичноMлежит на биссектрисе углаACB. Следовательно,M– центр вписанной окружности треугольникаABC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь