Олимпиадная задача по планиметрии: неравенство площадей в прямоугольнике для 8-9 классов
Задача
Пусть M – внутренняя точка прямоугольника ABCD, а S – его площадь. Докажите, что S ≤ AM·CM + BM·DM.
Решение
Заметим, что площадь прямоугольника ABCD равна удвоенной сумме
площадей треугольников BMC и AMD. При параллельном переносе на вектор 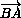 треугольник BMC перейдёт в равный ему треугольник AND. Поэтому S = 2SAMDN ≤ AM·DN + AN·DM = AM·CM + BM·DM. (Мы воспользовались неравенством из задачи 132076.)
треугольник BMC перейдёт в равный ему треугольник AND. Поэтому S = 2SAMDN ≤ AM·DN + AN·DM = AM·CM + BM·DM. (Мы воспользовались неравенством из задачи 132076.)
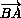
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет