Олимпиадная задача по планиметрии: угол ABM внутри квадрата для 8–9 класса
Задача
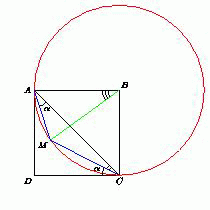
Внутри квадрата ABCD выбрана такая точка M, что ∠MAC = ∠MCD = α. Найдите величину угла ABM.
Решение
Поскольку ∠DCM = ∠MAC < 45°, точка M лежит внутри треугольника ACD. Рассмотрим описанную окружность треугольника AMC. В силу того же равенства углов, DC – касательная к этой окружности (точки D и A лежат по разную сторону от хорды MC). Поэтому центр окружности – пересечение прямой CB и серединного перпендикуляра к диагонали AC, то есть совпадает с B. Следовательно, ∠ABM = 2∠ACM = 90° – 2α.
Ответ
90° – 2α.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет