Олимпиадная задача: точки пересечения медиан треугольников внутри квадрата

Пусть K, L, P и N – середины сторон AB, BC, CD и AD соответственно. Тогда KLMN – квадрат. Поскольку точка пересечения медиан делит каждую медиану треугольника в отношении  2 : 1,  считая от вершины, то при гомотетии с центром M и коэффициентом ⅔ четырёхугольник KLMN переходит в четырёхугольник с вершинами в точках пересечения медиан треугольников ABM, BCM, CDM и DAM. Значит, последний четырёхугольник также является квадратом.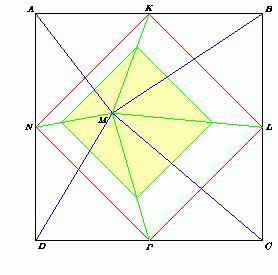

Ответ задачи отсутствует