Олимпиадная задача: длина периода суммы бесконечных десятичных дробей (дроби, 9-11 класс)

  Как известно, длина минимального периода дроби является делителем длины любого другого ее периода, (длину минимального периода конечной десятичной дроби мы будем считать равной единице).

  Лемма. Если k – длина одного из периодов (не обязательно минимального) каждой из дробей A и B, то k будет длиной некоторого периода дробей  A + B  и  A – B.

  Доказательство. Периодическую дробь A с длиной периода k можно представить в виде  A = 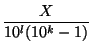, где X – целое число. Аналогично

B = .  Без ограничения общности можно считать, что  l ≥ m.  Тогда  A + B = 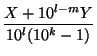.  Это число такого же вида, так что соответствующая дробь имеет период длины k.

  Доказательство для  A – B аналогично.   Пусть дробь A имеет период длины 6, а дробь B – период длины 12. Из леммы следует,что 12 – длина некоторого периода дроби  A + B.  Значит, длина минимального периода дроби  A + B является делителем числа 12.

  С другой стороны, длина периода дроби  A + B  не может равняться 6 - иначе дробь  B = (A + B) – A  имела бы период длины 6. Значит, длина минимального периода дроби  A + B  не может равняться 6, 3, 2 и 1.

  Остаются два варианта: 12 и 4. Покажем, что оба эти варианта возможны:

A = 0,(000001),  B = 0,(000000000001),  A + B = 0,(000001000002);

A = 0,(000001),   B = 0,(011100110110),  A + B = 0,(0111).

Ответ задачи отсутствует