Олимпиадная задача по алгебраическим неравенствам для 8-10 классов — доказательство неравенства для a, b и c
Задача
Положительные числа a, b и c таковы, что abc = 1. Докажите неравенство
Решение
Решение 1: Обозначим a = x³, b = y³, c = z³. Тогда xyz = 1. Поскольку x² – xy + y² ≥ xy, имеем x³ + y³ ≥ (x + y)xy, откуда
Решение 2: После приведения к общему знаменателю и раскрытия скобок (с учётом того, что abc = 1) неравенство принимает вид
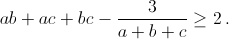
Полученное неравенство очевидно, так как согласно неравенству Коши
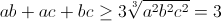 и
и 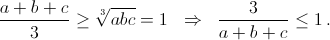
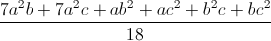  , как среднее арифметическое 18 чисел (одночлены с коэффициентом 7 рассматриваются как сумма 7 равных слагаемых). Применив неравенство Коши, получим
 , как среднее арифметическое 18 чисел (одночлены с коэффициентом 7 рассматриваются как сумма 7 равных слагаемых). Применив неравенство Коши, получим
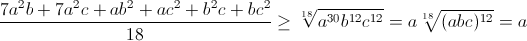 , или
, или 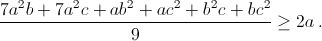
Умножив (**) на c/b и заменив 1/b на ac, получим ac2 + bc ≥ 2c. (2)
Аналогично a²c + ab ≥ 2a, (3)
b²c + ab ≥ 2b. (4)
Можно считать, что числа расположены в порядке возрастания: a ≤ b ≤ c. Тогда a ≤ 1 ≤ c и (c – 1)(c – a²) ≥ 0. Раскрыв скобки, получим
a² + c² ≥ a²c + c. Умножая на b и заменяя abc на 1, получим, наконец, неравенство a²b + bc² ≥ bc + a. (5)
Складывая неравенства (1) – (5), получим неравенство (*).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь