Олимпиадная задача по планиметрии для 8–9 класса от Маркелова С.В.: Касательные из точки пересечения диагоналей трапеции
Задача
Диагонали трапеции ABCD пересекаются в точке K. На боковых сторонах трапеции, как на диаметрах, построены окружности. Точка K лежит вне этих окружностей. Докажите, что длины касательных, проведённых к этим окружностям из точки K, равны.
Решение
Пусть боковые стороны трапеции – это стороны AB и CD. Обозначим через M и N вторые точки пересечения прямых AC и BD и окружностей с диаметрами AB, CD соответственно (см. рис.). Если прямая AC касается окружности с диаметром AB, то мы полагаем M = A, аналогично поступим, если прямая BD касается соответствующей окружности.
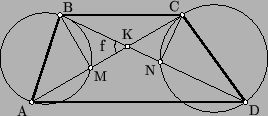
M = A или N = D. Значит, надо доказать, что KM·KA = KN·KD. (*)
Первый способ. Поскольку угол AMB опирается на диаметр, ∠KMB = 90°. Это верно и в случае M = A, так как касательная перпендикулярна радиусу, проведенному в точку касания. Обозначим величину угла AKB через φ. Тогда KM = KB cos φ, KN = KC cos φ. Подставляя полученные формулы в (*), находим, что нужно доказать равенство KB·KA = KC·KD. Это известное свойство трапеции следует из подобия треугольников AKD и CKB.
Второй способ. Так как ∠BMC = 90° = ∠BNC, точки B, M, N и C лежат на окружности с диаметром BC, откуда ∠CMN = ∠CBN = ∠BDA (так как
BC || AD). Но тогда ∠AMN + ∠NDA = 180°, поэтому точки A, M, N, D лежат на одной окружности. По теореме о произведении отрезка секущей на её внешнюю часть KM·KA = KN·KD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь