Олимпиадная задача по планиметрии для 8–10 класса: равенство отрезков MP и NQ (Нагель И. П.)
Задача
Две окружности пересекаются в точках A и B. В точке A к обеим проведены касательные, пересекающие окружности в точках M и N. Прямые BM и BN пересекают окружности еще раз в точках P и Q (P – на прямой BM, Q – на прямой BN). Докажите, что отрезки MP и NQ равны.
Решение
Решение 1: Пусть окружности расположены как на рисунке.
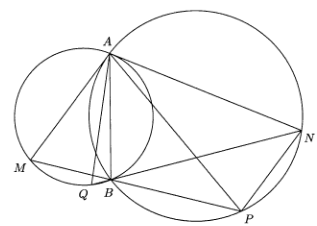
При этом ∠MAN = ∠BAM + ∠BAN = ∠ANB + ∠BAN = ∠ABQ. Поэтому ⌣AQ = 2∠ABQ = 2∠MAN = ⌣ABM. Значит, равны и хорды AQ и AM. Поэтому треугольники AQN и AMP не только подобны, но и равны, и MP = NQ.
Решение 2: По теореме о секущей и касательной MP = AM²/MB, NQ = AN²/NB, то есть достаточно доказать, что AM² : AN² = MB : NB. (*)
Из теоремы об угле между касательной и хордой следует, что треугольники AMB и NAB подобны (см. рис.). Значит, AM : AN = AB : NB
и AM : AN = MB : AB. Перемножая, получаем равенство (*).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь