Олимпиадная задача: сумма чисел в квадратной таблице степеней двойки (8-10 класс)
Задача
Таблица имеет форму квадрата со стороной длины n. В первой строчке таблицы стоит одно число – 1. Во второй – два числа – две двойки, в третьей – три четвёрки, и т.д.:
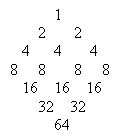
Решение
(1 + 2 + 4 + ... + 2n) + (2 + 4 + ... + 2n + 1) + ... + (2n + 2n+1 + ... + 22n) =
= (1 + 2 + ... + 2n) + 2(1 + 2 + ... + 2n) + ... + 2n(1 + 2 + ... + 2n) = (1 + 2 + ... + 2n)².
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет