Олимпиадная задача по планиметрии: вписанный треугольник и точки на окружности
Задача
ТреугольникABCвписан в окружность. ТочкаD— середина дугиAC, точкиKиLвыбраны на сторонахABиCBсоответственно так, чтоKLпараллельнаAC. ПустьK' иL' — точки пересечения прямыхDKиDLсоответственно с окружностью. Докажите, что вокруг четырехугольникаKLL'K' можно описать окружность.
Решение
Рассмотрим касательнуюNMв точкеD(рис. 1). Имеем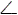
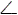K'KL=KDM,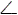K'L'D=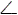K'DN. ОтсюдаK'KL+K'L'L= 180o, а это и означает, что вокруг четырёхугольникаKK'L'Lможно описать окружность.
 |
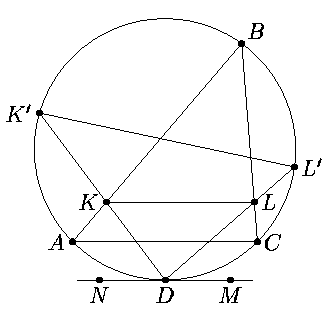| Рис. 1 |
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет