Можно ли из выпуклого четырехугольника вырезать параллелограмм? Олимпиадная задача, планиметрия, 7-9 класс
Задача
Из всякого ли выпуклого четырехугольника можно вырезать параллелограмм, три вершины которого совпадают с тремя вершинами этого четырехугольника?
Решение
Рассмотрим произвольный четырёхугольникABCD. Т. к.
A+B+C+D= 360o, то либоA+B≥ 180o, либоC+D≥ 180o. Аналогично, либоB+C≥ 180o, либоD+A≥ 180o. Пусть, без ограничения общности,A+B≥ 180oиB+C≥ 180o. Тогда рассмотрим параллелограмм с вершинамиA,B,Cи сторонамиABиBC. ПустьE— его четвёртая вершина. ТогдаABC+BCE= 180o≤ABC+BCD. Аналогично,ABC+BAE= 180o≤ABC+BAD. Отсюда следует, что отрезкиCEиEAлежат внутри или на сторонах четырёхугольникаABCD.
 |
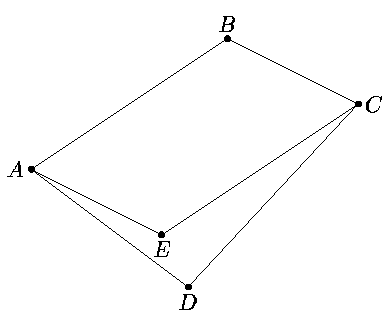| Рис. 1 |
Ответ
Да, из всякого.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет