Олимпиадная задача по математике: оптимальный выбор коробок с конфетами (9-11 класс)

  Пусть  a₁ ≤ a₂ ≤ ... ≤ a_n  – массы конфет в коробках стоимостью в 1, 2, ..., n  у. е. соответственно, а  n₁ < n₂ < ... < n_k  – номера тех коробок, которые нужно купить.

  1. Обозначим  m_j = ^jn/_k  (j = 1, ..., k)  и докажем, что для искомого набора номеров должны быть выполнены неравенства  n_j ≥ m_j.      (*)

  Действительно, предположим, что  n_j < m_j  для некоторого j.

  Тогда, например, в случае a₁ = ... = a_nj = n_j < a_{nj + 1} = ... = a_n = n + n_j

получаем

     a₁ + ... + a_n = n_j² + (n – n_j)(n + n_j) = n²,

     a_n1 + ... + a_nk = (k – j)(n + n_j) + jn_j < (k – j)n + nj = kn,

то есть нарушено требование задачи.

  2. Пусть теперь все неравенства (*) верны. Докажем, что тогда требование задачи выполнено.

  а) При  n = 10,  k = 3  имеем  n₁ ≥ ¹⁰/₃,  n₂ ≥ ²⁰/₃,  n₁ ≥ 10,  т.е. достаточно взять 4-ю, 7-ю и 10-ю коробки. И действительно:

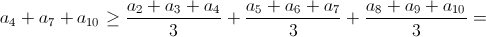
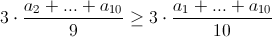
(добавив к группе чисел число, меньшее их всех, мы уменьшим среднее арифметическое).   б) Положим  n₀ = m₀ = a₀ = 0  и возьмём целые числа   n_j = m_j + ε_j,  где  0 ≤ ε < 1.   Рассмотрим ступенчатую функцию, задаваемую равенствами  f(x) = a_j  при  j – 1 < x ≤ j.  Поскольку функция не убывает, её среднее значение на промежутке уменьшается, когда оба конца промежутка сдвигают влево (даже с изменением длины промежутка). (Среднее значение – это площадь под графиком функции на заданном промежутке, деленная на длину этого промежутка.) В частности,

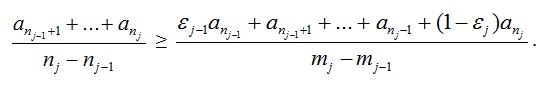
  Поэтому

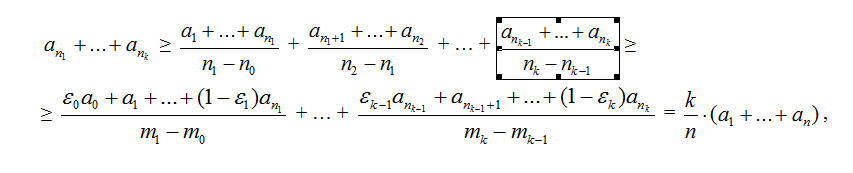
так как все знаменатели равны ⁿ/_k,  n_k = m_k = n,  ε_k = 0.

  Итак, стоимость набора из k коробок, удовлетворяющего требованию задачи, будет наименьшей для наименьших целых чисел n_j, удовлетворяющих неравенствам (*).

Коробки стоимостью   а)  4, 7 и 10 у. е.;   б) 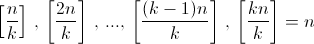   у. е.