Олимпиадная задача по теории чисел. Последовательности, делимость, 9-11 класс
Задача
В возрастающей бесконечной последовательности натуральных чисел каждое число, начиная с 2002-го, является делителем суммы всех предыдущих чисел. Докажите, что в этой последовательности найдётся некоторое число, начиная с которого каждое число равно сумме всех предыдущих.
Решение
Пусть n > 2000, Sn = a1 + ... + an – сумма n первых членов и dnan+1 = Sn. Тогда dn+1an+2 = Sn+1 = Sn + an+1 = (dn + 1)an+1. Так как an+2 > an+1, то
dn+1 < dn + 1, то есть dn+1 ≤ dn (это целые числа). Таким образом, последовательность dn не возрастает. Достаточно доказать, что в этой последовательности каждое число d, кроме 1, может встретиться только конечное число раз.
Пусть dn = dn+1 = ... = dn+k = d. Согласно полученной выше формуле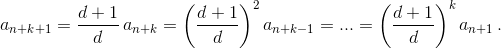 
Числа d и d + 1 взаимно просты, а an+1 может делиться только на конечную степень d.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь