Олимпиадная задача Гальперина: подобие цветных раскрасок в квадрате и круге
Задача
Можно ли раскрасить все точки квадрата и круга в чёрный и белый цвета так, чтобы множества белых точек этих фигур были подобны друг другу и множества чёрных точек также были подобны друг другу (возможно, с различными коэффициентами подобия)?
Решение
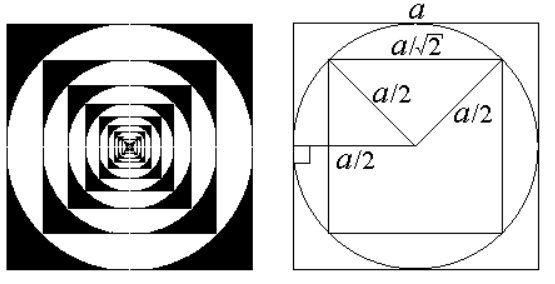 Рассмотрим такую раскраску квадрата: впишем круг в квадрат и раскрасим в
чёрный цвет точки квадрата, лежащие вне круга; впишем в полученный круг квадрат
со сторонами, параллельными сторонам исходного квадрата. Раскрасим в белый цвет
точки круга, лежащие вне "маленького" квадрата. По такому же правилу раскрасим
маленький квадрат и т. д. Заметим, что мы считаем граничные точки лежащими
"внутри" фигуры. Таким образом, граница каждого квадрата покрашена чёрным, за
исключением четырёх точек касания вписанного в квадрат круга, а граница каждого
круга - белым, за исключением четырёх вершин квадрата, вписанного в этот круг.
Пусть сторона исходного квадрата равна a, тогда сторона маленького
квадрата равна a/21/2. Следовательно, длины сторон квадратов
стремятся к 0. Поэтому все точки, кроме центра, будут раскрашены. Центр
раскрасим в чёрный цвет.
Очевидно, что множество чёрных точек квадрата подобно множеству чёрных точек
круга, вписанного в этот квадрат (второе получается из первого гомотетией с
центром в центре квадрата и с коэффициентом 1/21/2. А множество белых
точек квадрата просто совпадает с множеством белых точек вписанного в него
круга.
Рассмотрим такую раскраску квадрата: впишем круг в квадрат и раскрасим в
чёрный цвет точки квадрата, лежащие вне круга; впишем в полученный круг квадрат
со сторонами, параллельными сторонам исходного квадрата. Раскрасим в белый цвет
точки круга, лежащие вне "маленького" квадрата. По такому же правилу раскрасим
маленький квадрат и т. д. Заметим, что мы считаем граничные точки лежащими
"внутри" фигуры. Таким образом, граница каждого квадрата покрашена чёрным, за
исключением четырёх точек касания вписанного в квадрат круга, а граница каждого
круга - белым, за исключением четырёх вершин квадрата, вписанного в этот круг.
Пусть сторона исходного квадрата равна a, тогда сторона маленького
квадрата равна a/21/2. Следовательно, длины сторон квадратов
стремятся к 0. Поэтому все точки, кроме центра, будут раскрашены. Центр
раскрасим в чёрный цвет.
Очевидно, что множество чёрных точек квадрата подобно множеству чёрных точек
круга, вписанного в этот квадрат (второе получается из первого гомотетией с
центром в центре квадрата и с коэффициентом 1/21/2. А множество белых
точек квадрата просто совпадает с множеством белых точек вписанного в него
круга.
Ответ
Можно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь