Олимпиадная задача: целые значения тангенсов углов треугольника (планиметрия, 9-11 класс)

  Наименьший угол треугольника не превосходит 60°, поэтому его тангенс может равняться только 1 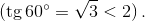   Значит, сумма двух оставшихся углов равна 135°. Далее можно рассуждать по-разному.   Первый способ. Наименьший из этих двух углов не может равняться 45° (иначе третий угол равен 90°), но он не больше 67,5°, поэтому его тангенс меньше 3 (если  tg φ = 3,  то  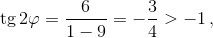   значит,  2φ > 135°).  Следовательно, его тангенс равен 2. Тангенс последнего угла находится как тангенс суммы двух первых углов, взятый с противоположным знаком:  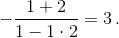   Второй способ. Пусть  tg α = m,  tg β = n.  Тогда     то есть  m + n = mn – 1.  Записав это уравнение в виде  (m – 1)(n – 1) = 2,  видим, что один из множителей равен 1, а второй – 2.

1, 2 и 3.