Олимпиадная задача по стереометрии: расположение 2001 многогранника без тройных пересечений

Решение 1:   Положим  N = 2001  и опишем построение расположения N выпуклых многогранников, из которых никакие три не пересекаются и каждые два касаются.

  Рассмотрим бесконечный круговой конус, вершина O которого находится в начале координат, а ось направлена вдоль оси Oz. На окружности, являющейся сечением конуса плоскостью  z = 1,  возьмём вершины A₁, A₂, ..., A_N правильного N-угольника. Обозначим через B₁, B₂, ..., B_N середины меньших дуг A₁A₂, A₂A₃, ..., A_NA₁ соответственно. Через C(t) обозначим круг, являющийся сечением конуса плоскостью  z = t,  через O^t – центр этого круга, через 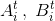    – точки пересечения образующих OA_i, OB_i с кругом C(t), где  t > 0,  1 ≤ i ≤ N. 

  Лемма. Пусть выпуклый многоугольник M лежит внутри круга C(t₀),  t₀ > 0.  Рассмотрим бесконечную вверх "призму" P, основанием которой служит многоугольник M, а боковое "ребро" параллельно прямой OB_i для некоторого i. Многоугольник (равный M), который получается при пересечении призмы P и круга C(t), обозначим M(t) (таким образом, M(t₀) совпадает с M). 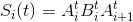Тогда найдётся такое положительное  T > t₀,  что при всех  t > T  многоугольник M(t) будет содержаться внутри сегмента     круга C(t).

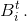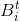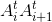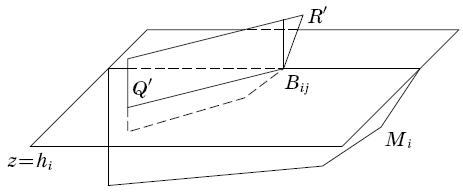
  Доказательство. Многоугольник M(t) является образом M при параллельном переносе на вектор, параллельный образующей OB_i. Поэтому многоугольник M(t) содержится внутри круга, равного кругу C(t₀), который касается круга C(t) в точке     Расстояние от точки     до прямой     прямо пропорционально длине образующей 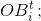    следовательно, найдётся такое T, что при всех  t > T  это расстояние больше диаметра окружности C(t₀) (см. рис.). Это и означает, что многоугольник M(t) попадает внутрь сегмента S_i(t) круга C(t).   Переходим к индуктивному построению нашего расположения.

  Выберем  t₁ > 0.  Возьмём выпуклый многоугольник M₁ внутри круга C(t₁). Рассмотрим бесконечную вверх "призму" P₁, основанием которой служит многоугольник M₁, а боковое "ребро" параллельно прямой OB₁.

  Пусть для некоторого n  (1 ≤ n < N)  уже определены положительные числа  t₁ < t₂ < ... < t_n–1,  выпуклые многоугольники M₁, ..., M_n–1, лежащие внутри кругов С(t₁), С(t₂), ..., С(t_n–1), бесконечные "призмы" P₁, P₂, ..., P_n–1 с основаниями M₁, M₂, ..., M_n–1 и боковыми "рёбрами", параллельными OB₁, OB₂, ..., OB_n–1 соответственно.

  Согласно лемме, существует такое  t_n > t_n–1,  что многоугольник M₁(t_n) содержится внутри сегмента S₁(t_n) круга C(t_n), многоугольник M₂(t_n) содержится внутри сегмента S₂(t_n) круга C(t_n), ..., многоугольник M_n–1(t_n) содержится внутри сегмента S_n–1(t_n) круга C(t_n).

  Сдвинем каждую из прямых 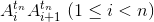    в направлении вектора  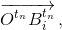   пока она не совпадёт с прямой l_i(t_n), касающейся многоугольника M_i(t_n). Теперь построим выпуклый многоугольник М_n, который содержится в круге C(t_n), касается каждого многоугольника M_i(t_n) и лежит по разные с ним стороны от прямой l_i(t_n): возьмём для каждого i одну из точек касания многоугольника M_i(t_n) и прямой l_i(t_n); при  n > 3  эти точки являются вершинами выпуклого (n–1)-угольника, который и выберем в качестве M_n; при  n = 2, 3  надо добавить ещё несколько точек).

  Рассмотрим бесконечную вверх "призму" P_n, основанием которой является многоугольник M_n, а боковое "ребро" параллельно прямой OB_n. Построение будет закончено, когда мы получим призмы P₁, P₂, ..., P_N. Наконец, "срежем" призмы плоскостью  z = T,  где  T > t_N.

  Докажем, что полученные (обычные) призмы удовлетворяют условию задачи. Для этого достаточно показать, что призма P_n пересекается с призмой P_i

(i < n)  только в плоскости круга C(t_n). Пусть, напротив, найдётся общая точка  R ∈ C(t)  двух призм, где  t > t_n. Через точку R проведём прямые, параллельные OB_n и OB_i; обозначим их точки пересечения с плоскостью круга C(t_n) через R_n и R_i соответственно. Тогда точка R_n должна принадлежать многоугольнику M_n(t_n), а точка R_i – многоугольнику M_i(t_n). Ясно, что (ненулевые) векторы 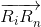    и 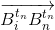    противоположно направлены. Однако это невозможно, поскольку точки R_i и     лежат по одну сторону от прямой l_i(t_n), а точки R_n и 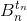    – по другую. Противоречие.

Решение 2:

  Опишем построение расположения произвольного количества выпуклых многогранников, удовлетворяющих условию.

  Схема построения. Построим несколько вертикальных пересекающихся плоскостей π_i, а в каждой из них – по выпуклому многоугольнику M_i так, чтобы

  а) верхняя граница каждого многоугольника состояла из одного горизонтального ребра, и её вертикальная проекция совпадала с проекцией всего многоугольника;

  б) высоты h_i верхних границ возрастали с возрастанием номера;

  в) при движении по нижней границе многоугольника "вправо" (то есть с увеличением абсциссы) точка поднималась вверх;

  г) для каждой пары многоугольников их единственная общая точка лежала на верхней границе многоугольника с меньшим номером и на нижней границе многоугольника с бóльшим номером.

  Детальное построение. Рассмотрим в горизонтальной плоскости  z = 0  прямые l_i:  y = i(x – i),  i = 1, 2, ..., n.  Заметим, что прямые l_i и l_j  (i < j)  пересекаются в точке  A_ij(i + j, ij).  Эти точки различны, и для каждого i абсциссы точек A_1i, A_2i, ..., A_i–1,i, A_i,i+1, ..., A_in строго возрастают. π_i – вертикальная плоскость, содержащая прямую l_i.

  Для каждого  i < n  поднимем точки A_i,i+1, ..., A_in на одинаковую высоту h_i. Полученные точки обозначим B_i,i+1, ..., B_in. Высоты подберём так, чтобы для каждого  i > 2  ломаные B_1iB_2i...B_i–1,iB_in были выпуклыми вниз (для этого нужно лишь, чтобы h_i было достаточно велико по сравнению с h_i–1; например, подойдёт  h_i = n^i–1, поскольку n больше отношения длин любых отрезков одной прямой с концами в точках A_ij).

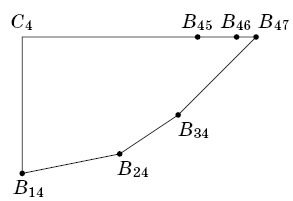
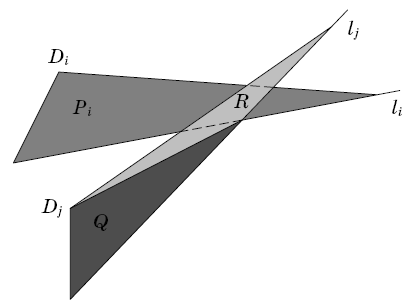
  Построим еще для каждого i  (1 < i < n)  точку C_i над A_1i на высоте h_i. Многоугольники  M₃ = C₃B₁₃B₂₃B_3n,  M₄ = C₄B₁₄B₂₄B₃₄B_4n,  ...,

M_n–1 = C_n–1B_1,n–1B_2,n–1...B_n–2,n–1B_n–1,n выпуклы (на левом рисунке изображен многоугольник M₄ для  n = 7).

  Плоскости π_iи π_j (i < j)  пересекаются по вертикальной прямойm_ij, проходящей через точкуB_ij. При этом точки многоугольникаM_iрасположены не выше точкиB_ij, аM_jсодержит только отрезок прямойm_ij, находящийся выше точкиB_ij. ПоэтомуB_ij– единственная общая точкаM_iиM_j. Как видим, многоугольникиM_iудовлетворяют всем свойствам, описанным в схеме построения.   Осталось построить многогранники-пирамиды с основаниямиM_i (2 <i < n).  Сделаем вершинами пирамид серединыD_iотрезковС_i–1С_i. ТочкаD_iлежит правее всех плоскостей с меньшим номером и левее остальных, а её высота большеh_i–1и меньшеh_i. Покажем, что пирамидыP_iс вершинамиD_iи основаниямиM_iудовлетворяют условию задачи.   Пусть  i < j.  Через общую точкуM_iиM_jпроведём вертикальную прямую. Она разобьетM_jна две части – левуюQ'и правуюR'(рис. справа). Как видим, правая часть находится над плоскостью  z = h_i,  касаясь её в точкеB_ij. Соответственно, и пирамидаP_jразобьется на две пирамиды: "левую"Qи "правую"R(нижний рис.). ПирамидаQотделена отP_iвертикальной плоскостью π_i: за исключением общей точки, все вершиныQлевее, а вершины пирамидыP_i– правее этой плоскости.Rотделена отP_iгоризонтальной плоскостью на высотеh_i: за исключением общей точки, все вершиныRвыше, а вершиныP_i– ниже или на этой плоскости (на рисунке проекцииP_iиQнаходятся по разные стороны от прямойl_i). Таким образом, пирамидыP_iиP_jимеют единственную общую точку.

Ответ задачи отсутствует