Олимпиадная задача по планиметрии: углы и равные хорды в окружности (8-10 класс)
Задача
В окружности с центром O проведены три равные хорды AB, CD и PQ (см. рисунок). Докажите, что MOK равен половине угла BLD.
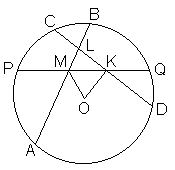
Решение
Докажем вспомогательное утверждение: через точку внутри окружности, отличную от центра, можно провести не более двух хорд равной длины. "Алгебраическое доказательство".Пусть через точку Z проходят три хорды длины a. Для каждой из них произведение отрезков, на которые их делит точка Z, постоянно и равно, допустим, m. Расмотрим одну из хорд. Пусть точка Z делит эту хорду на отрезки длины x1и x2. Тогда x1+ x2= a, x1* x2= m, следовательно, числа x1и x2 корни уравнения x2- ax + m = 0. Корнями того же уравнения будут длины отрезков, на которые точка Z разбивает остальные две хорды. Но у этого уравнения только два корня, а это означает, что каждая из хорд точкой Z разбивается в точности на отрезки длиной x1и x2. Это значит, что окружность с центром Z радиуса x1имеет с данной окружностью по крайней мере три общие точки. Тогда она обязана с ней совпадать, но Z не центр исходной окружности. Противоречие. "Геометрическое доказательство".Равные хорды одной окружности опираются на равные дуги, поэтому они переводятся друг в друга поворотом вокруг центра O этой окружности. Следовательно, эти хорды равноудалены от точки O, поэтому касаются некоторой окружности с центром О. Из данной точки к данной окружности можно провести не более двух касательных.
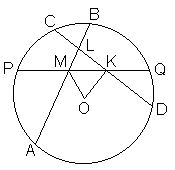
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь