Олимпиадная задача по планиметрии: биссектриса и высота треугольника, Рубанов И. С.
Задача
Один из углов треугольника на 120° больше другого.
Докажите, что биссектриса треугольника, проведённая из вершины третьего угла, вдвое длиннее, чем высота, проведённая из той же вершины.
Решение
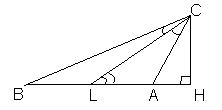
Пусть ABC – данный треугольник, ∠B = α, ∠A = 120° + α. Тогда ∠C = 60° – 2α. Если CL – биссектриса, то ∠CLA = ∠LCB + ∠LBC = 30°. Пусть CH – высота, тогда в треугольнике CLH катет CH, лежащий против угла в 30°, в два раза меньше, чем гипотенуза CL.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет