Олимпиадная задача по планиметрии: ортоцентр, окружность и пересечения, 8-10 класс
Задача
Пусть H – ортоцентр треугольника ABC, X – произвольная точка. Окружность с диаметром XH вторично пересекает прямые AH, BH, CH в точках A1, B1, C1, а прямые AX, BX, CX в точках A2, B2, C2. Доказать, что прямые A1A2, B1B2, C1C2 пересекаются в одной точке.
Решение
Рассмотрим для определенности случай, когда точки расположены на окружности в порядке A1B2C1A2B1C2. Пусть XH = d. Тогда
A1B2 = d sin∠A1HB2 = d sin∠XBC, так как HA1 ⊥ BC, а HB2 ⊥ BX (см. рис.). Следовательно,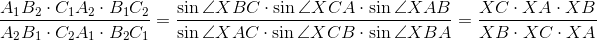 
= 1, что согласно задаче 135216 равносильно доказываемому утверждению (см. рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет