Олимпиадная задача по планиметрии: две пересекающиеся окружности и касательные
Задача
Две окружности радиуса 1 пересекаются в точках X, Y, расстояние между которыми также равно 1. Из точки C одной окружности проведены касательные CA, CB к другой. Прямая CB вторично пересекает первую окружность в точке A'. Найти расстояние AA'.
Решение
Пусть B' – точка пересечения первой окружности Ω с прямой CA, O – её центр, O' – центр другой окружности Ω'. Прямая CO' – биссектриса угла ACB, поэтому пересекает Ω в середине K дуги A'B'. Степень точки O' относительно Ω равна O'O² – OС² = 2, значит, O'K·O'C = 2. Пусть ∠A'CO' = γ, тогда
sin γ = O'B/CO' = 1/CO', а A'K = 2 OC sin γ = 2/CO' = O'K. По лемме о трезубце (см. задачу 155381) O' – центр вневписанной окружности треугольника A'CB', то есть прямая A'B' касается окружности Ω' в некоторой точке C'.
Следовательно, ∠A'O'A = ∠AO'C' + ½ C'O'B = ∠CB'A' + ½ CA'B', ∠O'A'O = ∠O'A'B' + ∠B'A'O = π/2 – ∠C'O'A' + π/2 – ∠BCA = π – ∠BCA – ½ CA'B' = ∠CB'A' + ½ CA'B'. Так как O'A = OA', AO'A'O – равнобедренная трапеция, и AA' = OO' = ![]() (см. рис.).
(см. рис.).
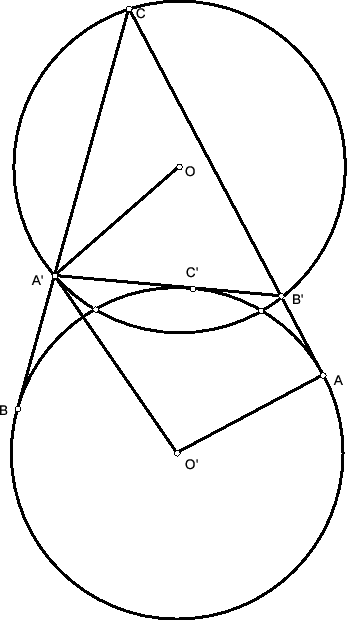
Ответ
![]() .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь