Назад

Олимпиадная задача по планиметрии: доказательство для двух параллельных хорд в окружности

Задача 203932 • Сложность: 3 • 8-10 класс
Задача

В окружности с центром O проведены две параллельные хорды AB и CD. Окружности с диаметрами AB и CD пересекаются в точке P.

Доказать, что середина отрезка OP равноудалена от прямых AB и CD.

Авторы:
Заславский А. А.
Разделы:
Планиметрия
Источники:
I Олимпиада по геометрии имени И.Ф. Шарыгина (2005 г.) 10 класс Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина
Количество версий:
5
Решение

Пусть  R = OA  – радиус первой окружности, X, Y – середины AB и CD, Q – середина OP. Тогда

XQ² = ¼ (2OX² + 2XP² – OP²) = ¼ (2OX² + 2XA² – OP²) = ¼ (2R² – OP²) = YQ².  Таким образом, Q равноудалена от точек X и Y, а, значит, и от прямых AB и CD (см. рис.).

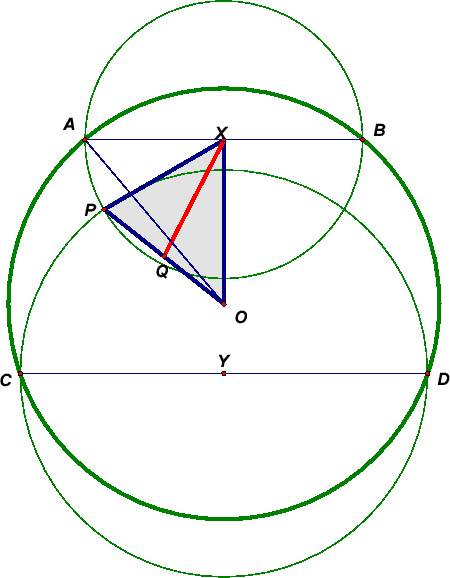
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет