Олимпиадная задача: Числа на вершинах куба – принцип крайнего, 6-8 классы
Задача
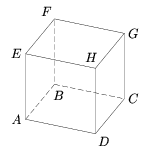
В вершинах кубаABCDEFGHрасставлены натуральные числа так, что числа в соседних (по ребру) вершинах отличаются не более чем на единицу. Докажите, что обязательно найдутся две диаметрально противоположные вершины, числа в которых отличаются не более чем на единицу. (Пары диаметрально противоположных вершин куба: A и G, B и H, C и E, D и F.)
Решение
Обозначим числа, стоящие в вершинахA,B,C,D,E,FиHкуба, соответствующими маленькими латинскими буквами:a,b,c,d,e,f,gиh. Возьмём одну из вершин, в которой стоит наименьшее число. Без ограничения общности это вершинаAи в ней стоит числоa. (оно находится в вершине A). Тогда для значений чиселb,dиe, стоящих в соседних сAвершинахB,DиE, остаётся только две возможностиaиa+ 1. Значит, какие-нибудь два из чиселb,dиeравны. Пусть равные числа стоят в вершинахBиE(остальные случаи рассматриваются аналогично). В этом случае искомыми будут диаметрально противоположные вершиныEи C:e=b, а числаcиbотличаются не более чем на 1, поэтому числаeиcотличаются не более чем на 1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь