Олимпиадная задача: заяц и охотники на кубе — решение по комбинаторной геометрии (7-8 класс)
Задача
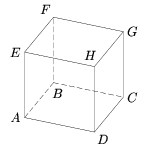
В одной из вершин кубаABCDEFGHсидит заяц, но охотникам он не виден. Три охотника стреляют залпом, при этом они могут ''поразить'' любые три вершины куба. Если они не попадают в зайца, то до следующего залпа заяц перебегает в одну из трёх соседних (по ребру) вершин куба. Укажите, как стрелять охотникам, чтобы обязательно попасть в зайца за четыре залпа. (В решении достаточно написать четыре тройки вершин, в которые последовательно стреляют охотники.)
Решение
Покажем, что последовательность выстреловCFH,BDE,DEGиACFприводит к цели. Покрасим вершины A, C, F и H в чёрный цвет, а остальные вершины — в белый. Заметим, что любые две соседние вершины будут покрашены в разные цвета. Значит, после каждого залпа заяц перебегает в вершину другого цвета.
Сделаем первый залп по вершинам C, F и H. Если заяц находился в чёрной вершине, то либо охотники сразу попали в него, либо заяц находился в вершине A. В последнем случае после залпа заяц перебежит в одну из трёх соседних вершин, и залп (BDE) обязательно достигнет цели.
Если заяц находился в белой вершине, то после двух выстрелов он снова окажется в белой вершине. Рассуждая аналогично предыдущему случаю, убеждаемся, что залпы (DEG), а потом (ACF) обязательно поразят зайца.
Есть и другие решения.
Ответ
(CFH), (BDE), (DEG), (ACF). (Порядок залпов важен!)
Чтобы оставлять комментарии, войдите или зарегистрируйтесь