Олимпиадная задача по планиметрии и комбинаторной геометрии: разрезание пятиугольника на остроугольные треугольники
Задача
Можно ли разрезать на четыре остроугольных треугольника
а) какой-нибудь выпуклый пятиугольник,
б) правильный пятиугольник.
Решение
а) См. рисунок.
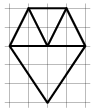
Ответ
а) Можно; б) нельзя.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет