Олимпиадная задача по планиметрии 7 класса: найти сторону квадрата (Шарыгин И. Ф.)
Задача
Фигура на рисунке
составлена из квадратов. Найдите сторону
левого нижнего, если сторона самого маленького равна 1.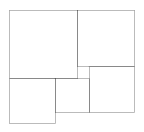
Решение
Заметим, что сторона самого большого квадрата равна сумме сторон двух квадратов: следующего за ним по часовой стрелке и самого маленького. Обозначив сторону самого большого квадрата через x, последовательно выразим стороны других квадратов —x- 1,x- 2,x- 3 (см. рисунок). Сторону левого нижнего квадрата нам выразить черезxне удалось, поэтому придётся обозначить её черезy. Теперь заметим, что верхняя сторона прямоугольника равнаx+ (x- 1), а нижняя —(x- 2) + (x- 3) +y. Но ведь противоположные стороны прямоугольника равны. Получаем уравнение
x + (x - 1) = (x - 2) + (x - 3) + y.
Отсюда2x- 1 = 2x- 5 +yи, значит,y= 4.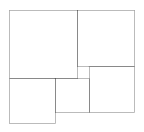
Ответ
4.00
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет