Олимпиадная задача по комбинаторике: минимум школьников в астрономическом кружке
Задача
В одной из школ 20 раз проводился кружок по астрономии. На каждом занятии присутствовало ровно пять школьников, причём никакие два школьника не встречались на кружке более одного раза. Докажите, что всего на кружке побывало не менее 20 школьников.
Решение
Решение 1: Всего было 20·5 = 100 посещений кружка. Если каждый школьник посетил кружок не более четырёх раз, то всего школьников было не менее чем
100 : 4 = 25.
Пусть теперь хотя бы один школьник посетил кружок пять раз. Тогда на каждом из этих пяти занятий все остальные школьники разные. Их уже 5·4 = 20.
Решение 2: Из пяти школьников можно составить ровно 10 пар. Так как пары не повторялись, то всего кружок посетили 10·20 = 200 различных пар. Но из 19 школьников можно составить только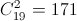 
различную пару.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь