Олимпиадная задача Ященко: битва фишек Вани и Серёжи на доске 4×6 для 7 класса
Задача
На доске 4×6 клеток стоят две чёрные фишки (Вани) и две белые фишки (Серёжи, см. рис.). Ваня и Серёжа по очереди двигают любую из своих фишек на одну клетку вперёд (по вертикали). Начинает Ваня. Если после хода любого из ребят чёрная фишка окажется между двумя белыми по горизонтали или по диагонали (как на нижних рисунках), она считается "убитой" и снимается с доски. Ваня хочет провести обе свои фишки с верхней горизонтали доски на нижнюю. Может ли Серёжа ему помешать?
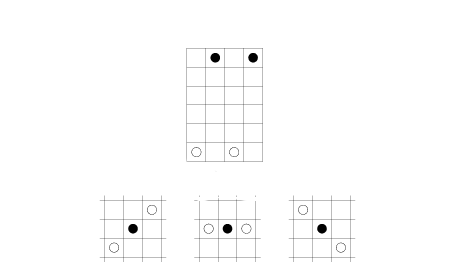
Решение
Будем двигать среднюю Ванину фишку вперёд, не обращая внимания на ходы Серёжи.
Назовём номер горизонтали, на которой фишка стоит (считая снизу), её высотой. Если Ванина фишка окажется между Сережиными, то её высота h будет равна полусумме высот Серёжиных фишек.
Пусть это произошло после хода Серёжи. Значит, ребята сделали равное число ходов – по n, и сумма высот Серёжиных фишек равна n + 2, а высота Ваниной равна 6 – n. Получаем n + 2 = 12 – 2n, то есть 3n = 10, что неверно, так как 10 не делится на 3.
Пусть Ванину фишку "зажали" после его хода. Значит, Ваня сделал на один ход больше – Серёжа сделал n ходов, а Ваня – n + 1. Тогда сумма высот Серёжиных фишек равна n + 2, а высота Ваниной равна 6 – n – 1. Получаем n + 2 = 10 – 2n, или 3n = 8, что тоже неверно.
Следовательно, средняя фишка пройдет на нижнюю горизонталь. Теперь двигаем крайнюю фишку, которую зажать вообще нельзя.
Ответ
Не может.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь