Олимпиадная задача на математическую логику и теорию чисел для 7–8 классов: расшифровка примера с чётными и нечётными числами
Задача
Расшифровать пример на умножение, если буквой Ч зашифрованы чётные числа, а буквой Н – нечётные.

Решение
Запишем пример в виде
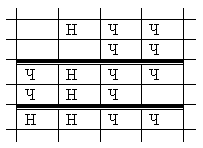
Ответ
348·28 = 9744.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет