Олимпиадная задача по математике для 7-8 классов: восстановление примера на умножение
Задача
Умножение чисел.Восстановите пример на умножение натуральных чисел, если известно, что сумма цифр у обоих сомножителей одинакова.
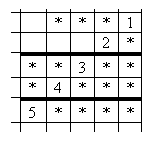
Решение
Обратите внимание на последнюю фразу. Перепишем пример в следующем виде
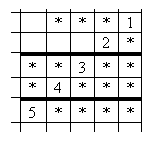
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет