Олимпиадная задача по планиметрии для 8–9 класса: углы в треугольнике ABC с высотой BH
Задача
В треугольнике ABC с углом B, равным 50°, и стороной BC = 3 на высоте BH взята такая точка D, что ∠ADC = 130° и AD = 
.
Найдите угол между прямыми AD и BC, а также угол CBH.
Решение
Пусть точка D' симметрична точке D относительно прямой AC. Тогда ∠B + ∠AD'C = ∠B + ∠ADC = 180°. Значит, четырёхугольник ABCD' – вписанный.
Согласно задаче 155463 D – ортоцентр треугольника ABC. Следовательно, AD ⊥ BC.
Из подобия прямоугольных треугольников AHD и BHC следует, что AH : BH = AD : BC = : 3. Значит, ∠ABH = 30°. Следовательно,
∠CBH = ∠B – ∠ABH = 50° – 30° = 20°.
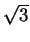
Ответ
90°, 20°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет