Олимпиадная задача по планиметрии и комбинаторной геометрии для 8–11 классов: максимальная разность черных и белых треугольников в раскраске выпуклого многоугольника
Задача
Выпуклый N-угольник разбит диагоналями на треугольники (при этом диагонали не пересекаются внутри многоугольника). Треугольники раскрашены в чёрный и белый цвета так, что каждые два треугольника с общей стороной раскрашены в разные цвета. Для каждого N найдите максимум разности количества белых и количества чёрных треугольников.
Решение
Сначала оценим значение разности (приведём два способа). Первый способ. При разбиении на треугольники диагоналями получится N – 2 треугольника (см. задачу 158154). К каждой из N – 3 проведённых диагоналей примыкает чёрный треугольник, поэтому их не меньше чем ⅓ (N – 3). Следовательно, белых треугольников не больше
N – 2 – (N/3 – 1) = 2N/3 – 1, а искомая разность не больше 2N/3 – 1 – (N/3 – 1) = N/3.
В случае N = 3k + 1 количество чёрных треугольников не меньше k (как целое число, большее ⅓ (N – 3) = k – ⅔), и разность, соответственно, не больше N – 2 – 2k = k – 1. Второй способ. Количество сторон белых треугольников не более чем на N превышает количество сторон чёрных, так как внутри многоугольника количество сторон совпадает, а на границе сторон всего N. Поэтому разность количеств белых и чёрных треугольников не превосходит N/3. В случае
N = 3k + 1 заметим, что чётность этой разности равна чётности суммы, то есть чётности числа N (и, следовательно, разность не может равняться k).
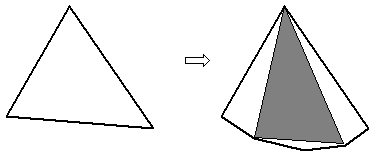
Теперь приведём примеры, показывающие, что требуемые значения разности достигаются. При N = 3, 4, 5 эти значения равны 1, 0 и 1; примеры очевидны, и в каждом есть белый треугольник, примыкающий к стороне N-угольника. Осталось заметить, что при увеличении числа сторон на три можно увеличить значение разности на 1, заменив один из таких примыкающих белых треугольников на шестиугольник, разрезанный, как показано на рис.:
Ответ
k при N = 3k и N = 3k + 2, k – 1 при N = 3k + 1.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь