Олимпиадная задача по алгебраическим неравенствам и тригонометрии для 10–11 классов
Задача
Пусть x, y, z – любые числа из интервала (0, π/2). Докажите неравенство 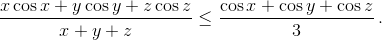
Решение
Несложно преобразовать исходное неравенство к равносильному: (x – y)(cos x – cos y) + (x – z)(cos x – cos z) +(y – z)(cos y – cos z) ≤ 0.
Последнее верно, поскольку в силу убывания косинуса каждое из трёх слагаемых неположительно.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет