Олимпиадная задача по числам: существуют ли иррациональные a и b, чтобы [a^m] ≠ [b^n] для всех натуральных m и n?

  Первый пример. 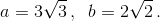    Заметим, что  x³ – y³ > x² – y²  при  x > y > 1.  Поэтому  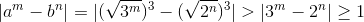   (последнее неравенство следует из разной чётности чисел 3^m и 2ⁿ). Отсюда, очевидно, следует утверждение задачи.   Второй пример.  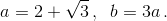   Положим  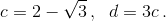   Из формулы бинома следует, что число  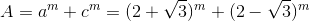   целое и не кратно 3 (члены, содержащие нечётную степень  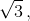  сокращаются; все слагаемые, кроме 2^m, кратны 3).

  В то же время число  B = bⁿ + dⁿ = 3ⁿ(aⁿ + cⁿ)  также целое и кратно 3.

  Но  0 < c < d < 1,  поэтому  [a^m] = A – 1 ≠ B – 1 = [bⁿ].

Существуют.