Олимпиадная задача: Найти точки A и B на графиках y = x³ и y = x³ + |x| + 1 с минимальным расстоянием
Задача
Верно ли, что на графике функции y = x³ можно отметить такую точку A, а на графике функции y = x³ + |x| + 1 – такую точку B, что расстояние AB не превысит 1/100?
Решение
Решение 1: Положим c = 100³ + 100 + 1,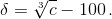 
Поскольку (100 + δ)³ = с, точки A(100 + δ, c) и B(100, c) лежат на соответствующих графиках. При этом AB = δ. Но 3·100²·δ < (100 + δ)³ – 1003 = 101, то есть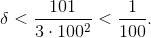 
Решение 2: Положим δ = 0,01. Найдётся такое положительное число x, что точки A(x + δ, (x + δ)³) и B(x, x³ + x + 1) имеют одинаковые ординаты (тогда AB = δ).
Действительно, (x + δ)³ = x³ + x + 1 ⇔ 3x²δ + (3δ²– 1)x + δ³ – 1 = 0. Поскольку свободный член отрицателен, уравнение имеет два корня, причём разного знака.
Ответ
Верно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь