Олимпиадная задача: площадь и сдвиги треугольника на координатной плоскости (9–11 класс)

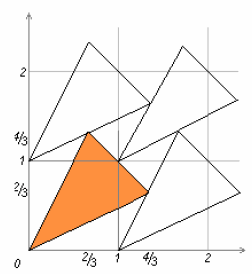
  а) Таким, например, является треугольник с вершинами в точках  (0, 0),  (⁴/₃, ⅔)  и  (⅔, ⁴/₃)  (см. рис.). Легко видеть, что стороны сдвинутых треугольников проходят через вершины исходного и что площадь треугольника равна ⅔.

  б) Лемма. Если многоугольник можно переносить на целочисленный вектор без самопересечений, то его площадь не больше 1.

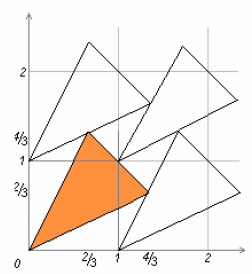
  Доказательство. Разрежем плоскость на единичные квадраты линиями координатной сетки. Наш многоугольник разрежется на несколько частей. Переведём все эти части (сдвигом на целочисленный вектор) в один квадрат. По условию, полученные фигуры не пересекаются, значит, их суммарная площадь не больше 1.   Пусть ABC – треугольник, удовлетворяющий условиям задачи. Обозначим через A₁, B₁ и C₁ соответственно середины сторон BC, CA и AB. Построим шестиугольник AC₁A₁CDE, где точки D и E получены отражением точек C₁ и A₁ относительно точки B₁ (см. рис.). Докажем, что этот шестиугольник можно переносить на целочисленный вектор без самопересечений.

  Предположим противное: наш шестиугольник при переносе на некоторый целочисленный вектор накладывается на себя. Рассмотрим точкуXшестиугольника, которая при этом движении попадает в точкуY, лежащую внутри шестиугольника. Если соединить точкуB₁со всеми вершинами шестиугольника, то получим шесть маленьких треугольничков.   Заметим, что точкиXиYнаходятся в противоположных (центрально симметричных относительноB₁) треугольничках. Действительно любые другие два треугольничка можно поместить в один большой треугольник, равныйABC(совпадающий сABC, центрально симметричныйABCили полученный из одного из них переносом на некоторый вектор). Такой треугольник, очевидно, также удовлетворяет условиям задачи и, следовательно, не может содержать “плохих” точекXиY.   Пусть, например, точкаXлежит в треугольничкеC₁A₁B₁, aY– в треугольничкеB₁DE. Сдвинем треугольникABCтак, чтобы он наложился на трапециюAC₁DE. Теперь начнём его двигать параллельноEDдо тех пор, пока не покроем трапециюA₁CDE. Поскольку при этом в каждый момент он целиком содержит треугольничекB₁DEи полностью "заметает" треугольничекC₁A₁B₁, то наступит момент, когда треугольник будет накрывать как точкуX, так и точкуY. Но и этот треугольник удовлетворяет условиям задачи. Противоречие.   По лемме площадь шестиугольника (равная  1,5S_ABC)  не больше 1. Следовательно,  S_ABC≤ ⅔.  Пример построен в a).

а) Может;  б) ⅔.