Назад

Олимпиадная задача по планиметрии: вневписанные окружности и середины в треугольнике ABC

Задача 198463 • Сложность: 2 • 10-11 класс
Задача

Вневписанные окружности касаются сторон AC и BC треугольника ABC в точках K и L. Докажите, что прямая, соединяющая середины KL и AB,

  а) делит периметр треугольника ABC пополам;

  б) параллельна биссектрисе угла ACB.

Решение

  Достроим чертеж до симметричного (см. рис.).

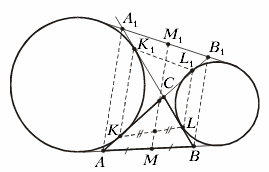
  Равнобочные трапецииAA1B1BиKK1L1Lобладают тем свойством, что основаниеAA1параллельно основаниюKK1и отстоит от него на то же расстояние, что иBB1отLL1. Это следует из равенства отрезков касательныхAKиBL(см. задачу155404) и угловCAA1иCBB1. Следовательно, средняя линияMM1трапецииAA1B1Bявляется также средней линией трапецииKK1L1L.   а)MM1делит диагональAB1трапецииAA1B1Bпополам, а половина этой диагонали равна полусумме сторонACиBCтреугольникаABC.   б)MM1параллельна биссектрисе углаACB.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет