Олимпиадная задача Канель-Белова: условие равносильности для многочленов и функций
Задача
Дана функция 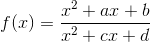 , где трёхчлены x² + ax + b и x² + cx + d не имеют общих корней. Докажите, что следующие два утверждения равносильны:
, где трёхчлены x² + ax + b и x² + cx + d не имеют общих корней. Докажите, что следующие два утверждения равносильны:
1) найдётся числовой интервал, свободный от значений функции;
2) f(x) представима в виде: f(x) = f1(f2(...fn–1(fn(x))...)), где каждая из функций fi(x) есть функция одного из видов: kix + bi, x–1, x².
Решение
Договоримся называть функцию, удовлетворяющую условию 1, дырявой, а условию 2 – представимой.
Мы будем рассматривать функции, определённые на всей числовой прямой, за исключением, быть может, конечного числа точек. Равенство функций мы будем понимать так, как это подразумевается в условии задачи, то есть равенство на общей области определения. Отметим, что замена функции на равную ей (в этом смысле) может изменить область значений только на конечное число точек, в частности, не может сделать дырявую функцию не дырявой, и наоборот.
Заметим, что данная нам функция не является дробно-линейной, так как равенство 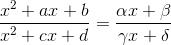 означало бы, что числитель и знаменатель левой части имеют общий множитель, после сокращения на который получается правая часть. Лемма. Пусть h(x) – дробно-линейная функция, g(x) – произвольная функция.
означало бы, что числитель и знаменатель левой части имеют общий множитель, после сокращения на который получается правая часть. Лемма. Пусть h(x) – дробно-линейная функция, g(x) – произвольная функция.
а) Функции g(x), g(h(x)) и h(g(x)) либо все представимы, либо все не представимы.
б) Функции g(x), g(h(x)) и h(g(x)) либо все дырявы, либо все не дырявы.
Доказательство. а) Очевидно, поскольку функция, обратная к дробно-линейной, является дробно-линейной.
б) Пусть g(x) не принимает значений в интервале I. Тогда g(h(x)) тем более не принимает значений в этом интервале. С другой стороны, в интервале I найдётся интервал J, целиком входящий в область определения функции h(x). В силу монотонности h(J) – тоже интервал, и функция h(g(x)) не принимает на нём значений в силу взаимной однозначности. Остальное следует из равенств g(x) = g(h(h–1(x))) = h–1(h(g(x))) и свойств дробно-рациональной функции. Итак, композиция с дробно-линейной функцией сохраняет дырявость и представимость. Это позволяет нам доказывать нужное свойство не для исходной функции, а для функции, упрощенной композициями с дробно-линейными функциями. 1) Докажем, что представимая функция дырява. Пусть функция 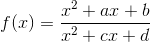 представима в указанном в условии виде
представима в указанном в условии виде
f1(f2(...fn–1(fn(x))...)) и k – наименьший номер, при котором fk(x) = x² (такая есть, иначе функция f(x) была бы дробно-линейной).
Тогда функция g(x) = fk(fk+1(...(fn(x))...) = (fk+1(...(fn(x))...)² дырява, так как не принимает отрицательных значений. С другой стороны,
h(x) = f1(f2(...fk–1((x))...)) является дробно-линейной функцией (как композиция дробно-линейных). Поэтому и f(x) = h(g(x)) – дырявая функция.
2) Теперь докажем, что дырявая функция представима. Пусть имеется интервал, не содержащий значений функции f(x).
Постараемся композициями c дробно линейными функциями максимально упростить вид функции f(x).
Вычтем из f(x) единицу и обратим дробь. Получится функция вида 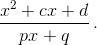 Если p = 0, то мы после умножения на q получаем функцию, представляющуюся в нужном виде: x² + cx + d = (x + с/2)² + d – c²/4.
Если p = 0, то мы после умножения на q получаем функцию, представляющуюся в нужном виде: x² + cx + d = (x + с/2)² + d – c²/4.
Если же p ≠ 0, то делаем линейную замену переменных z = px + q и получаем функцию вида 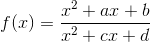 Вычтя B и разделив на A, получим окончательно функцию вида x + D/x (мы заменили z снова на x).
Вычтя B и разделив на A, получим окончательно функцию вида x + D/x (мы заменили z снова на x).
Заметим, что D ≠ 0 (в противном случае исходная функция f(x) была бы дробно-линейной). Кроме того, D не может быть отрицательным. Действительно, уравнение x + D/x = t приводится к виду x² – tx + D и при D < 0 имеет решение при любом t, что противоречит наличию интервала, свободного от значений функции f(x).
Таким образом, D = s², где s – некоторое положительное число.
Осталось заметить, что 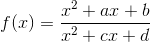 то есть эта "упрощённая" функция представима.
то есть эта "упрощённая" функция представима.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь