Может ли в параллелепипеде уместиться больший по размеру? Олимпиадная задача Шеня
Задача
Будем называть "размером" прямоугольного параллелепипеда сумму трёх его измерений – длины, ширины и высоты.
Может ли случиться, что в некотором прямоугольном параллелепипеде поместился больший по размеру прямоугольный параллелепипед?
Решение
Решение 1: Квадрат размера параллелепипеда с ребрами a, b, c равен (a + b + c)² = a² + b² + c² + 2(ab + ac + bc) = d² + S, где d – длина его диагонали, а S – площадь поверхности. Поэтому для отрицательного ответа достаточно доказать, что диагональ и площадь поверхности параллелепипеда P больше соответственно диагонали и площади поверхности лежащего внутри него параллелепипеда P'.
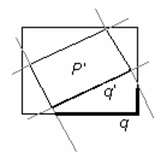
Неравенство для диагоналей сразу следует из того, что длина диагонали – наибольшее расстояние между точками параллелепипеда. Для доказательства неравенства между площадями поверхностей продолжим до бесконечности плоскости граней параллелепипеда P'. В результате поверхность параллелепипеда P разобьется на 14 частей. Из них шесть частей принадлежат полубесконечным параллепипедам, ограниченным каждый одной гранью P' и четырьмя продолжениями граней (на рисунке для простоты изображен плоский случай). Спроектируем каждую такую часть q на соответствующую грань q' (см. рис.). Эти проекции покроют поверхность P' полностью. Следовательно, суммарная площадь этих шести частей не меньше площади поверхности P'. Осталось заметить, что это не вся поверхность P.
Решение 2: Рассмотрим систему координат, начало которой находится в одной из вершин параллелепипеда P, а оси направлены по его рёбрам: ось Ox – по ребру длины a, ось Oy – по ребру длины b, Oz – по ребру длины c. Пусть u(u1, u2, u3), v(v1, v2, v3), и w(w1, w2, w3) – векторы, образованные рёбрами параллелепипеда P'. Тогда размер P' равен |u| + |v| + |w| ≤ |u1| + |u2| + |u3| + |v1| + |v2| + |v3| + |w1| + |w2| + |w3|.
Достаточно доказать, что |u1| + |v1| + |w1| ≤ a, |u2| + |v2| + |w2| ≤ b, |u3| + |v3| + |w3| ≤ c.
Пусть A – вершина параллелепипеда P' с наименьшей абсциссой (если таких несколько, то любая из них), B, C, D – соседние с ней вершины, а E – вершина, противоположная вершине A. Абсцисса вектора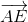 
не превосходит a. С другой стороны (поскольку 
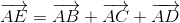), она равна сумме абсцисс векторов 
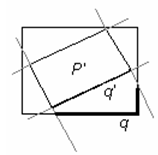Но (согласно выбору вершины A) эти абсциссы неотрицательны, то есть равны |u1|, |v1|, |w1|.
Остальные неравенства доказываются аналогично.
Ответ
Не может.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь