Олимпиадная задача по принципу Дирихле: конь, доска 8×8 и 17 клеток для 7–9 класса

Решение 1:   Разобьём доску на 16 одинаковых четырёхклеточных фигур: две из них закрашены на рисунке, еще две получим из них сдвигом вниз на две клетки, остальные получим из этих четырёх сдвигами вправо.

  Легко проверить, что ни из одной клетки такой фигуры нельзя попасть в другую менее чем за три хода коня. По принципу Дирихле какие-то две из 17 отмеченных клеток попадут в одну из этих фигур.

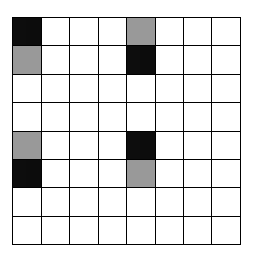
Решение 2:   Рассмотрим два случая.

  1) Среди отмеченных клеток есть клетки обоих цветов. Тогда клеток одного цвета (пусть чёрного) не меньше 9. Из отмеченной белой клетки конь за один ход может попасть только в 8 из них, а после двух ходов он окажется на белой клетке. Значит, для попадания в одну из отмеченных чёрных клеток ему нужно не менее трёх ходов.

  2) Все отмеченные клетки – одного цвета (пусть чёрные). Рассмотрим наименьший прямоугольник, содержащий все отмеченные клетки. Его площадь не меньше 33 (в нем не менее 17 чёрных клеток, а значит, не менее 16 белых). Поэтому одна из его сторон (пусть горизонтальная) не меньше 6. Тогда из отмеченной клетки, примыкающей к левой стороне прямоугольника конь не может за два хода попасть в отмеченную клетку, примыкающую к правой стороне.

Ответ задачи отсутствует