Олимпиадная задача по планиметрии: периметр многоугольника из n кругов, 10–11 класс
Задача
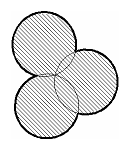
n бумажных кругов радиуса 1 уложены на плоскость таким образом, что их границы проходят через одну точку, причём эта точка находится внутри области, покрытой кругами. Эта область представляет собой многоугольник с криволинейными сторонами. Найдите его периметр.
Решение
Пусть P – точка, через которую проходят границы всех кругов. Соединим P с двумя соседними “вершинами” криволинейного многоугольника. Его “сторона” представляет собой дугу единичной окружности, поэтому её длина равна (выраженной в радианах) величине центрального угла, опирающегося на эту дугу, то есть в 2 раза больше величины вписанного угла APB. Таким образом, периметр многоугольника в 2 раза больше суммы углов, под которыми его стороны видны из точки P. Эти углы вместе составляют полный угол, величина которого равна 2π.
Ответ
4π.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь